The mirror formula

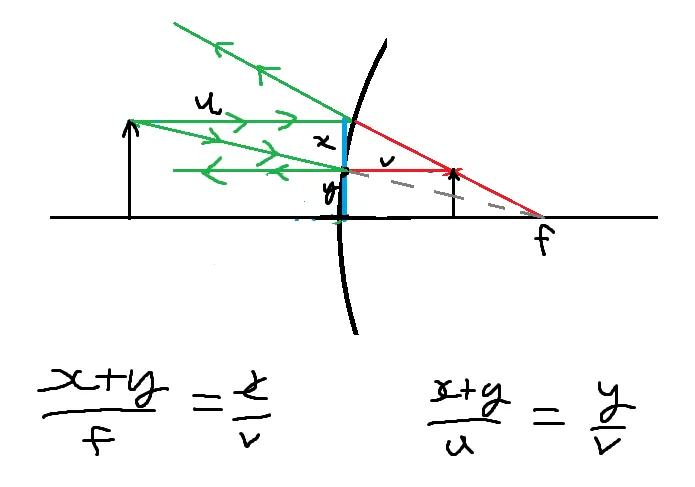
Consider the following setup, where an object is reflected off a concave mirror with focus at 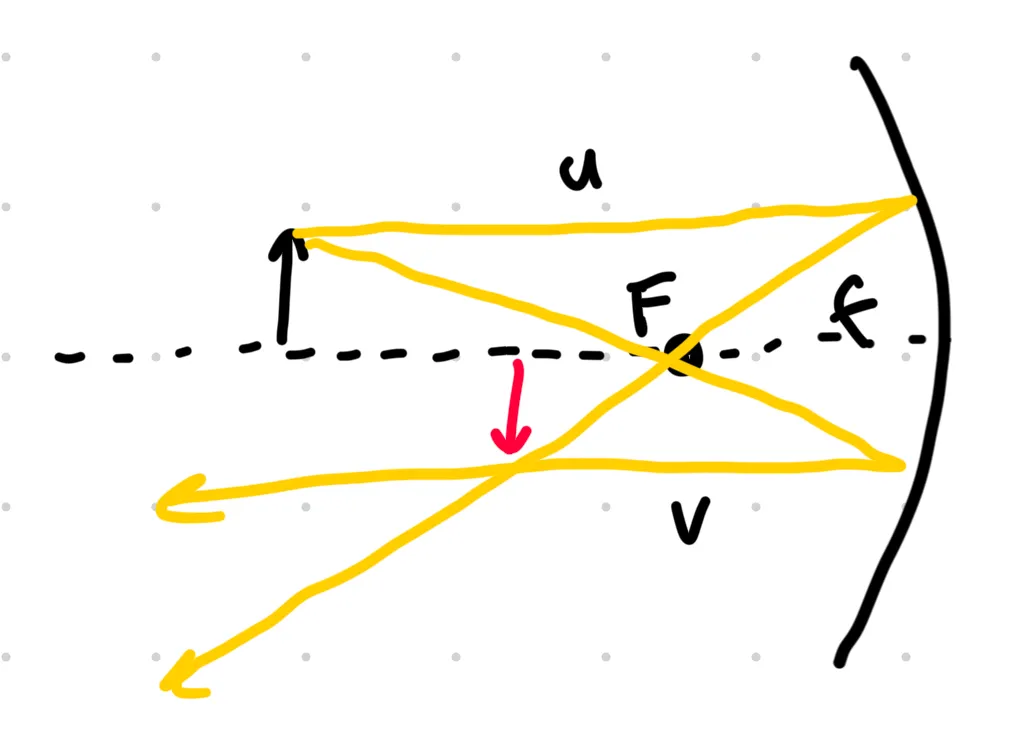$F$: Here, the black arrow represents the object, and the red arrow represents the image. $u$ and $v$ are then the object and image distances, respectively. Also, the focal length is denoted as $f$.

To relate these 3 variables, Physics 2 gives the following formula:

Before we go about deriving this relation, note that it is only an approximation, which increases in accuracy as the object height grows smaller. This is because when the object height is small, we can approximate the surface of the mirror as a flat plane, like so:

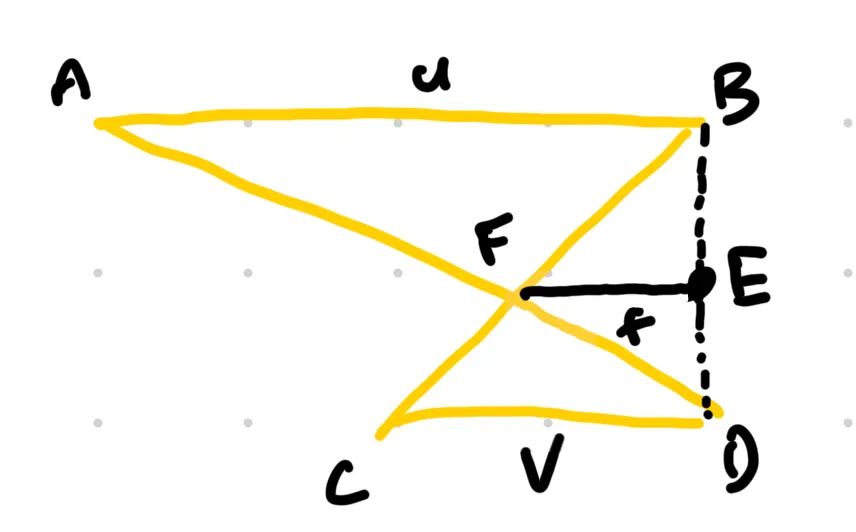
From here, the derivation of the mirror formula is extraordinarily elegant. Note that $\triangle BEF$ is similar to $\triangle BDC$, which means $BE = \frac{f}{v} \cdot BD$. Similarly, since $\triangle DEF \sim \triangle DBA$, we have $DE = \frac{f}{u} \cdot BD$. Adding these two results, we have that $BE + ED = (\frac{f}{v} + \frac{f}{u}) \cdot BD$. However, the left hand side is just $BD$, and hence:

Dividing by $f$ on both sides, we arrive at the mirror formula!

Note: I’m not actually sure if a similarly simple proof is possible for convex mirrors. If you know of one, please comment blow!

Edit: Here’s a similar proof for the convex mirror case, courtesy of u/jamesw73721 on Reddit: