Editorial: "Catch the Mole"

With problems like these, it’s often useful to consider extreme tree configurations, such as:

1. Long Chain

This case is easily solved via binary search.

2. Star Graph

Without the condition that the mole moves upward when our query misses, star graphs (i.e. trees of depth 1) would be impossible to solve in faster than $\mathcal{O}(N)$ queries. Luckily, the fact that the mole moves up means that we can actually solve any star graph in at most 2 queries!

So, it looks like if we want to figure out a worst-case scenario, we’ll need to balance out depth (long chains) and breadth (star graphs). One way we can achieve this is to construct a tree with $\mathcal{O}(\sqrt{N})$ chains of $\mathcal{O}(\sqrt{N})$ nodes connected to the root, like so: 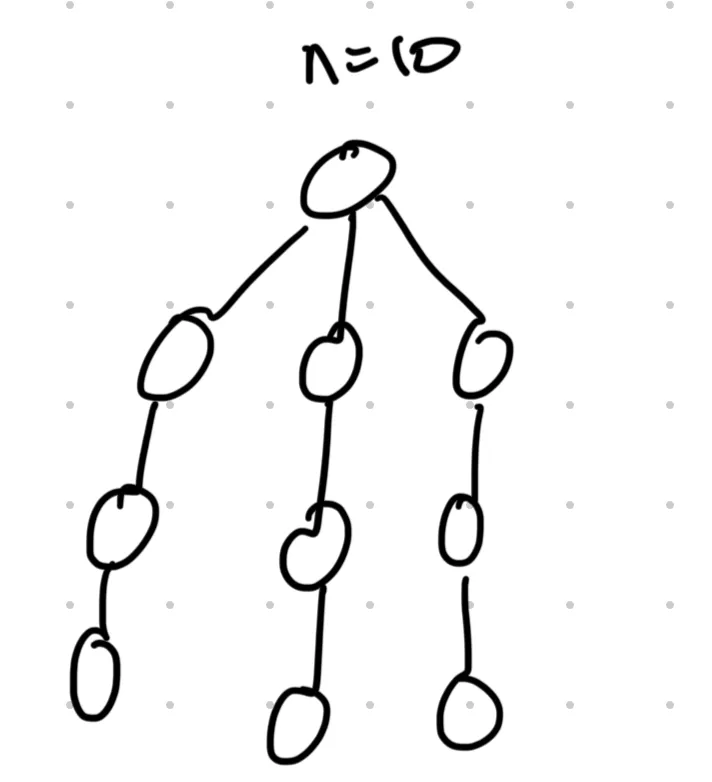Such a tree requires us to make $\mathcal{O}(\sqrt{N})$ queries in the worst case since we have to check all the branches, and in that time the mole may not reach the root.

So now the question becomes: can we always achieve this lower bound of $\mathcal{O}(\sqrt{N})$ queries?

As it turns out, yes! And an even more beautiful fact is that if, at every time-step, we simply make the query that eliminates as many nodes as possible, we can achieve this bound.

However, I’d first like to offer my slightly less elegant approach:

Let $S$ denote the set of leaves of the subgraph where the mole could currently be located---that is, the mole could be in any of these nodes, or their ancestors. The key idea is that we can always query a node $x$ such that we either

Reduce our search space to a single chain, to which we can apply a simple binary search.
Remove a single leaf from $|S|$ , then replace all elements of $S$ with their parents.

To select $x$ , we simply choose a leaf $y$ in $S$ , then set $x$ to be the highest ancestor of $y$ that contains only one leaf in 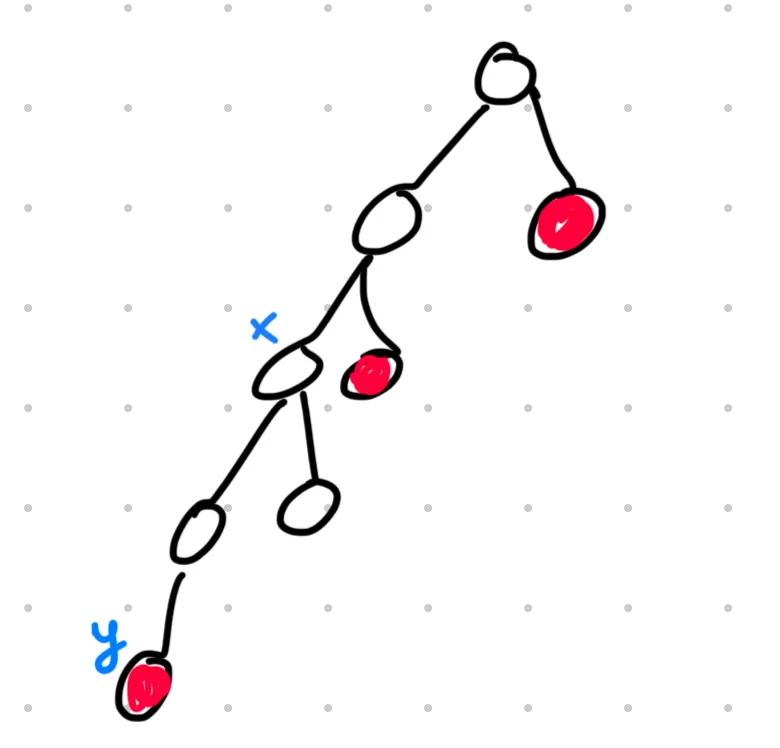$S$ . The red nodes denote the elements of $S$ . One possible choice of $x$ and $y$ is shown.

If we query $x$ and get response 1, we know the mole must be somewhere along the chain between $x$ and $y$ .

Otherwise, we eliminate $y$ from $S$ , and since the mole must move up, all elements of $S$ are replaced with their parents. 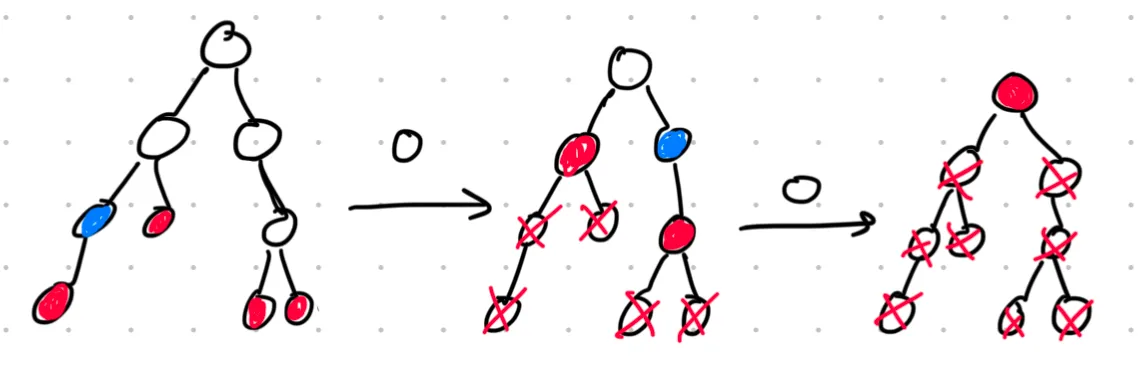An illustration of the process described above. Red nodes denote elements of $S$ , and the blue node denotes $x$ , the node we query in each step.

Let $S_i$ denote $S$ after the $i$ th query. Assume all queries have returned 0, since as soon as a query returns 1, we can find the mole in $\mathcal{O}(\log N)$ queries. Then, we have that

$|S_{i + 1}| < |S_i|$
All $S_i$ are disjoint, and thus $\sum |S_i| \leq N$

Combining these two facts, we can show that using our strategy, no more than $\mathcal{O}(\sqrt{N})$ queries can return 0. Thus, our total runtime is $\mathcal{O}(\sqrt{N} + \log N) = \mathcal{O}(\sqrt{N})$ .

The one thing I dislike about this approach is that a separate strategy (binary search) is needed to handle the chain case. However, this is not an issue for the strategy I mentioned above, where we always greedily eliminate as many nodes as possible. Here’s a nice proof for why this works, which I got from here:

Let’s consider a slight rephrasing of the problem. In each step, we can either 1) query a subtree and know whether it contains the mole or not, or 2) delete all leaves from the tree.

If we do operation 1 on a subtree of size $sz$ , we will eliminate, in the worst case, $\min(sz, N - sz)$ nodes. This means that, as long as there exists some subtree that is not “too small” nor “too large”, we can always eliminate a decent amount of nodes. However, let’s say this is not the case, and all subtrees are either too large or too small (for instance, a star graph). Then, there must exist a large subtree whose children are all small, and the root of this subtree must then have significant degree. This means the tree must have a significant number of leaves, which we can then eliminate via operation 2!

Let’s formalize this, and define a “small” subtree as one with size $\leq \sqrt{N}$ , and a “large” subtree as one with size $\geq N - \sqrt{N}$ . Then, if a large subtree has only small subtrees as children, its root must have a degree of at least $\frac{N - \sqrt{N}}{\sqrt{N}} = \sqrt{N} - 1$ , which means there must be at least $\sqrt{N} - 1$ leaves! Therefore, we can always remove at least $\mathcal{O}(\sqrt{N})$ nodes in each step, and so greedily maximizing the number of nodes deleted in each round suffices.

To summarize concisely why this approach works: unless some node has very high degree, a tree’s subtree sizes will be relatively continuous. IMO, a pretty elegant fact!